A feladat

Szerkesszük meg két adott pont által meghatározott szakasz felezőpontját csak körző használatával!

A megoldás

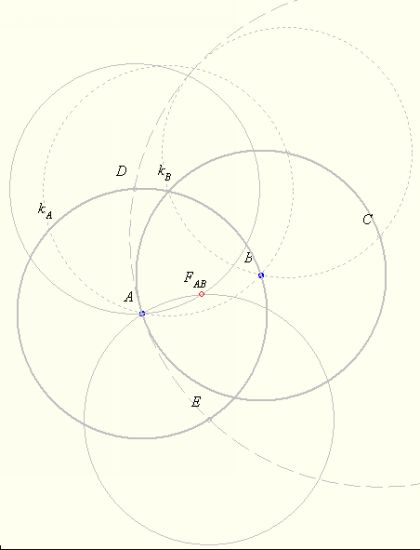
• Jelöljük a két adott pontot A, B-vel.
• Szerkesszük meg az A közepű és a B közepű AB sugarú köröket; jelöljük ezeket k_A-val, ill. k_B-vel (az ábrán a vastag szürke körök).
• Szerkesszük meg a k_B kör AB egyenesre illeszkedő átmérőjének A-tól kölönböző végpontját, és jelöljük ezt a pontot C-vel (ehhez AB-t kell A-ból kiindulva háromszor felmérni a k_B kör mentén; az ábrán a rövid szaggatott vonalú körök).
• Szerkesszük meg a C közepű AC sugarú kört (az ábrán a hosszú szaggatott vonalú kör), és jelöljük D-vel, E-vel ennek a körnek és k_A-nak a metszéspontjait.
• D-ből és E-ből körívezzünk a DA=AE=AB távolsággal (az ábrán a vékony szürke körök). A két körív A-tól különböző metszéspontja lesz az AB szakasz F_AB-vel jelölt felezőpontja.
• Ugyanis: az AB egyenesre vonatkozó szimmetria miatt F_AB illeszkedik az AB egyenesre. Az AF_ABD és DAC háromszögek hasonlók, mert egyenlőszárúak és az egyik alapon fekvő szögük megegyezik (nevezetesen a DAC szög). A hasonlóság aránya 1:2, mert 2AD=2AB=AC, ezért 2AF_AB=AD=AB.

A szerkesztés elvégzése az Euklides programmal

euklides.exe (kb. 2,5 MB) - az Euklides geometriai szerkesztőprogram letöltése