A feladat

Adott egy kör, a középpontja és egy pont a körön. Szerkesztendő olyan húrnégyzet a körbe csak vonalzó használatával, amelynek a körvonalon adott pont az egyik csúcsa!

A megoldás

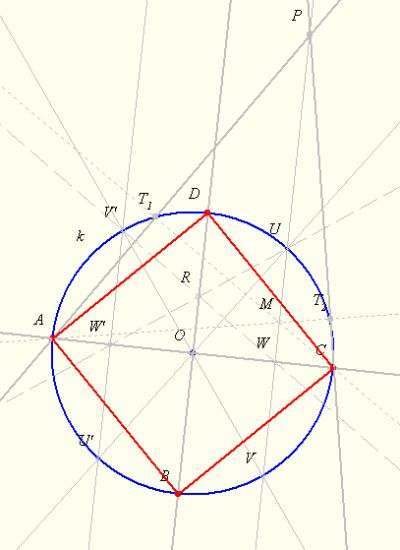
• Jelöljük a kör középpontját O-val, a körvonalon adott pontot A-val. Szerkesszük meg az OA egyenest. Ennek a körrel közös, A-tól különböző pontját jelöljük C-vel.
• Vegyünk fel egy P-vel jelölt segédpontot a körhöz A-ban, ill. C-ben húzott érintők által közrezárt síkrészben. Szerkesszük meg az AP, CP egyeneseket, ezeknek a körrel közös pontjait jelöljük T₁-gyel, ill. T₂-vel. Szerkesszük meg az AT₂, ill. CT₁ egyeneseket (az ábrán a rövid szaggatott vonalú egyenesek). Ezek Thálész tétele miatt merőlegesek a CP, ill. AP egyenesekre, így az APC háromszög magasságvonalaira illeszkednek, ezért az M-mel jelölt metszéspontjuk az APC háromszög magasságpontja. Ebből következőleg, a PM egyenes illeszkedik az APC háromszög P-ből induló magasságvonalára, tehát merőleges az AC szakaszra.
• A feladat megoldásához PM-mel párhuzamos egyenest kellene húzni az O-n keresztül. Ezt a következőképpen tehetjük meg. Jelöljük U-val, V-vel a PM egyenesnek a körrel, W-vel pedig az AC szakasszal vett metszéspontjait. Ekkor az UO egyenesnek a körrel vett új metszéspontja egyben U-nak O-ra vonatkozó tükörképe, ezért jelöljük U'-vel. Szerkesszük meg hasonlóan V-nek O-ra vonatkozó V' tükörképét. A középpontos tükrözés tulajdonságai miatt U'V' párhuzamos UV-vel. AC és U'V' metszéspontját jelöljük W'-vel. Könnyen látható, hogy az UWW'V' négyszög téglalap, amelyben O a WW' oldal felezőpontja. Az UW' és a WV' egyenesek a téglalap átlóegyenesei (az ábrán a hosszú szaggatott vonalú egyenesek), metszéspontjukat jelöljük R-rel. Ekkor az OR egyenes merőleges az AC átmérőre, ezért a körnek és OR-nek a közös pontjai a négyzet keresett B, D csúcsai. A szerkesztéshez csak vonalzó használatára volt szükség.

A szerkesztés elvégzése az Euklides programmal

(Az A pont a gravitáció bekapcsolásával - első ikonsor balról a nyolcadik ikon - illeszthető rá a körre.)

euklides.exe (kb. 2,5 MB) - az Euklides geometriai szerkesztőprogram letöltése